Cet article a été publié dans
le bulletin du photo-club Zoom92130 :
LES SECRETS DU NOMBRE D’OR
« Nul n’entre ici s’il n’est géomètre » (Platon)
La composition et les proportions.
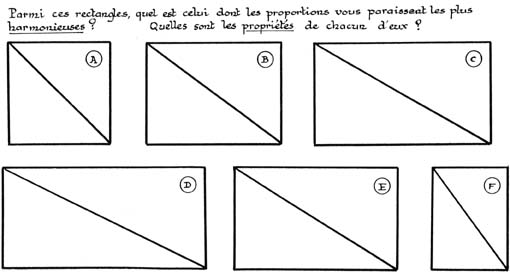
Ce petit test figure dans nombre de traités ou d’ouvrages d’initiation à l’esthétique. Et l’un de ces rectangles est plus souvent désigné que les autres. Notez donc vos réponses en essayant, pour chaque rectangle, de retrouver le tracé géométrique qui a défini ses proportions.
Si certaines proportions nous paraissent harmonieuses, ce n’est sans doute pas un simple effet du hasard. Nous trouvons beau ce que nous rencontrons fréquemment dans notre environnement, même sans le percevoir consciemment. Et parmi ces rapports de dimensions privilégiés, il est certaines constantes qui se retrouvent dans les différentes expressions de la vie animale ou végétale, et notamment dans le corps humain. Ainsi en est-il du visage humain, dont la hauteur est en moyenne un peu supérieure à une fois et demi la largeur. Cette même proportion se retrouve dans le règne végétal, et règle par exemple l’écartement des pousses et des feuilles le long d’un rameau.
Sous la complexité apparente des formes naturelles il n’est pas rare de retrouver un ordre, un rythme, qui ne relève pas du hasard. Observons l’élégante spirale d’un coquillage, la disposition régulière des graines sur le cœur de la fleur de tournesol, la savante géométrie d’un cristal de roche, tout ce qui nous entoure, jusqu’au merveilleux équilibre qui régit les mouvements des astres, semble bien réglé par des lois que l’esprit humain, depuis les origines, n’a eu de cesse de découvrir.
Cette harmonie naturelle, l’homme a d’instinct cherché à la retrouver dans ses créations. Dans une œuvre graphique simple, une photo en noir et blanc par exemple, la composition va s’exprimer par la répartition de surfaces de taille et de densité différentes. Lorsque nous composons une image, nous cherchons instinctivement à placer dans notre viseur les éléments avec un certain équilibre. L’analyse ultérieure de cette image nous fera découvrir que certains rapports de dimensions sont plus satisfaisants pour l’œil. Ces rapports sont les mêmes que ceux que l’on retrouve dans la nature. Et l’un de ces rapports se retrouve beaucoup plus souvent que les autres. Il est donc naturel que nos ancêtres aient été intrigués par cette proportion particulière qui règle notre visage et que les artistes tracent d’instinct dans leurs figures.
La magie du nombre
Nous appelons cette proportion particulière le nombre d’or (on l’appelle également “section d’or“, ou “divine proportion“). Il s’exprime bien sûr par une expression mathématique et l’on s’est depuis toujours attaché à en explorer toutes les propriétés. Et quand je dis depuis toujours, c’est que l’on trouve des traces de cette recherche dans les antiques légendes qui entourent la construction du temple de Salomon. Les pyramides d’Egypte comme la savante architecture des temples Grecs n’y ont pas échappé, et on le retrouve dans les secrets des bâtisseurs du Moyen-Age qui se sont transmis jusqu’à nous par les associations compagnonniques et les sociétés secrètes, dans la science des artistes de la Renaissance et des classiques, jusqu’aux études des philosophes et des théoriciens modernes.
L’architecte Le Corbusier l’a utilisé pour élaborer un outil de mesure (Le MODULOR) sur lequel il a réglé toutes ses constructions, et lui a consacré un ouvrage. Albert Einstein aurait dit à Le Corbusier que cet outil devait "rendre le mal difficile et le bien facile".
Bien entendu ce nombre est irrationnel (c’est-à-dire qu’il ne peut pas être déterminé avec un nombre fini de décimales). On l'exprime par la lettre grecque "phi" - c’est le nombre de Phidias (architecte et sculpteur grec, v. 490 – 431 av. J.-C.).
Il est égal à (1+√5)/2, soit environ 1,618. La figure suivante en montre le tracé géométrique et permet le calcul par le théorème de Pythagore.
Bien entendu, ce sujet fait l'objet de nombreux sites Internet. J'en ai remarqué un assez complet, quoique comportant quelques erreurs (notamment dans l'étude du Parthénon d'Athènes).
Vous pouvez le visiter ici.
Tracé géométrique du nombre d'or
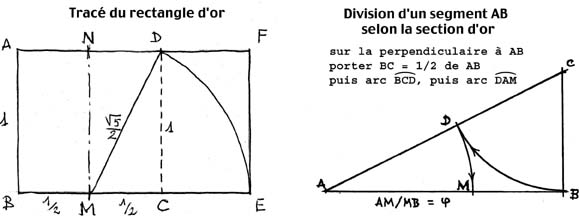
Soit un carré ABCD dont le coté est égal à 1. Soit M milieu de BC, traçons un arc de cercle de centre M et de rayon MD, pour rabattre cette longueur MD sur le prolongement du côté BC, ce qui définit le point E. Le rectangle ABEF est un rectangle d’or, c’est-à-dire que les proportions de ses cotés sont dans le rapport "phi".
En effet si le coté du carré initial AB = BC = 1, MC = 1/2. On applique le théorème de Pythagore pour calculer ME = MD = √ (MC²+CD²)
MD = √(1/2²+1²) soit √5/2 .
On a bien BE = BM+ME = 1/2+√5/2 ; le rapport des côtés du rectangle ABEF est égal à (1+√5)/2.
Une histoire de lapins …
Les propriétés de "phi" ne se limitent pas à exprimer une belle proportion, mais ouvrent la voie à une curiosité arithmétique, étudiée au début du XIIIe siècle par l’Italien Leonardo Fibonacci, dit Léonard de Pise (1175 - 1240). Ce riche commerçant s’intéressait aux mathématiques. Il avait voyagé au Moyen-Orient, où il avait pris connaissance du savoir des savants Arabes, dont il utilisait les chiffres et le zéro. Vraisemblablement grand amateur de lapins, il avait posé le problème suivant :
« Combien de paires de lapins peuvent être engendrées par une paire unique en UN an, si chaque mois, chaque paire produit une autre paire qui devient productive à son tour à partir du 2éme mois ? »
|
A la fin du premier mois, la paire originale A s’accouple, |
total 1 paire |
|
A la fin du second mois, la paire originale A produit une paire B1 |
total 2 paires |
| A la fin du troisième mois, la paire A produit une paire B2 - - - la paire B1 s’accouple, |
total 3 paires |
| A la fin du quatrième mois, la paire A produit une paire B3 - - - la paire B1 produit une paire C1 - - - - - - la paire B2 s’accouple |
total 5 paires |
| A la fin du cinquième mois, la paire A produit une paire B4 - - - la paire B1 produit une paire C2 - - - - - - la paire B2 produit une paire D1 - - - - - - - - - la paire B3 s’accouple |
total 8 paires |
| . . . etc… |
Je vous laisse le plaisir de continuer le détail du calcul qui doit vous conduire au résultat 233.
Mais remarquons la chose importante de ce calcul : le total à la fin de chaque ligne est la somme des totaux des deux lignes précédentes. Une telle suite de nombres est nommée suite de Fibonacci : 1 . 1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 . 89 . 144 . 233 …
Si l’on calcule le rapport entre deux termes successifs, on obtient :
1/1=1 ; 2/1=2 ; 3/2=1,5 ; 5/3=1,666 ; 8/5=1,6 ; 13/8=1,625 ; 21/13=1,615 ; 34/21=1,619 ; 55/34=1,6176 ; 89/55=1,618 ; 144/89=1,6179 ; 233/144=1,61805 … En progressant dans la suite on tend vers phi (chaque rapport est alternativement plus grand et plus petit que phi).
…et d’escargots.
Ne quittons pas la gastronomie, et créons donc une suite de Fibonacci en prenant pour termes de départ deux nombres en proportion d’or, par exemple 1 et phi (arrondi à la 3ème décimale) :
1 . 1,618 . 2,618 . 4,236 . 6,854 . 11,090 . 17,944 . 29,034 …etc.
Cette suite répond à la condition de Fibonacci puisque chaque terme est la somme des deux précédents, mais en même temps le rapport entre deux termes successifs est constant et égal à phi. C'est donc aussi une progression géométrique.
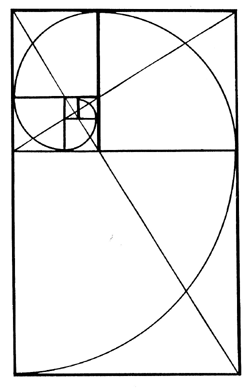
Appliquons cette progression en traçant une suite de rectangles, en partant d’un rectangle d’or et en traçant à chaque étape un carré sur le grand coté du rectangle précédent.
En traçant le quart de cercle inscrit dans chaque carré on obtient une spirale à pas croissant dont la courbe est très proche de celle que l’on trouve dans les coquillages et les végétaux.
Pour ne pas nous surcharger l’estomac, nous allons cesser là cette dissertation. Mais si vous y avez trouvé quelque intérêt, je vous montrerai une autre fois comment retrouver dans quelques exemples ces géométries cachées que l’on nomme « tracés régulateurs », et l’usage que nous pouvons en faire.
Au fait, avez-vous gagné ?
Revenons à notre petit test sur les rectangles ? Car ces six figures ne sont pas tracées au hasard, mais chacun de ces quadrilatères répond à des proportions bien précises. Et si le rectangle d'or se retrouve bien (en E), je vous livre maintenant les caractéristiques des cinq autres.
- A est le carré, figure de base ; ses 4 cotés sont égaux et sa diagonale = √2 (1,414)
- Dans le rectangle B, la longueur des cotés est respectivement de 3 et 4 ; sa diagonale est donc √(3²+4²) = 5 . Le triangle rectangle 3.4.5 est une figure particulière, qui permet de tracer un angle droit sans disposer d’une équerre, mais simplement avec un mètre, ou même avec une simple ficelle sur laquelle il suffit de faire 13 nœuds équidistants.
- Rectangle C : sa diagonale est égale au double du petit coté ; par conséquent si l’on dessine la figure symétrique par rapport au grand coté, le triangle ACE est équilatéral et la longueur BC = √3 (1,732)
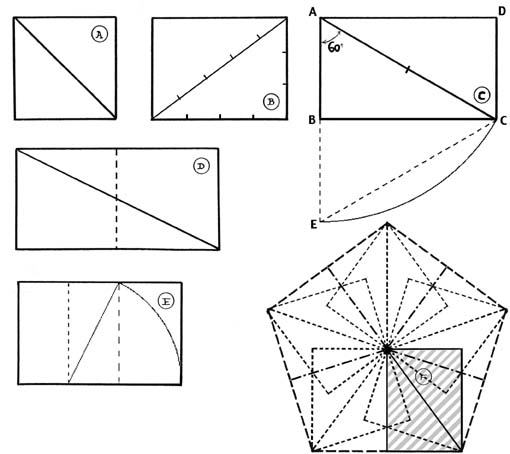
- Le rectangle D, c’est le double carré, de proportions 1/2, et qui servira de base à la construction de différents tracés régulateurs.
- Enfin le rectangle F nous ramène au chiffre 5, car on le retrouve dans la construction du pentagone régulier, donc de l'étoile à 5 branches ; le rapport de sa diagonale au petit coté est 2/phi. Et on pourrait encore imaginer beaucoup de constructions autour du 5, symbole de la sphère, de la matière et de la vie créative.

